선택 정렬
선택 정렬
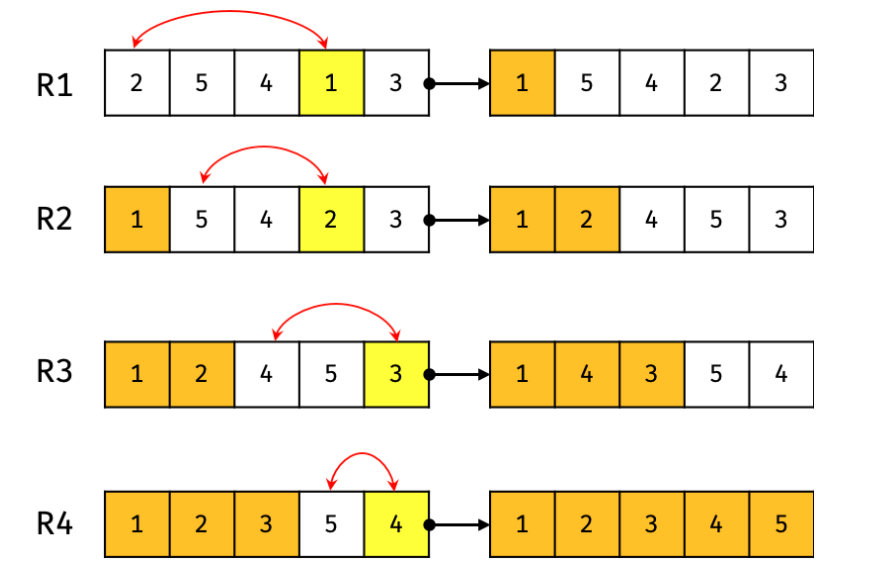
선택 정렬이란 제자리 정렬 알고리즘 중 한가지 방법이다. 보통 오름차순으로 정렬되는 선택 정렬은 다음과 같은 과정으로 이루어져 있다.
- 가장 작은 원소 값을 찾는다.
- 그 값을 맨 앞에 있는 값과 교체를 한다.
- 맨 처음 위치를 뺀 나머지 배열을 같은 방법으로 교체한다.
- 하나의 원소만 남을 때까지 위의 과정을 반복한다.
선택 정렬 예시
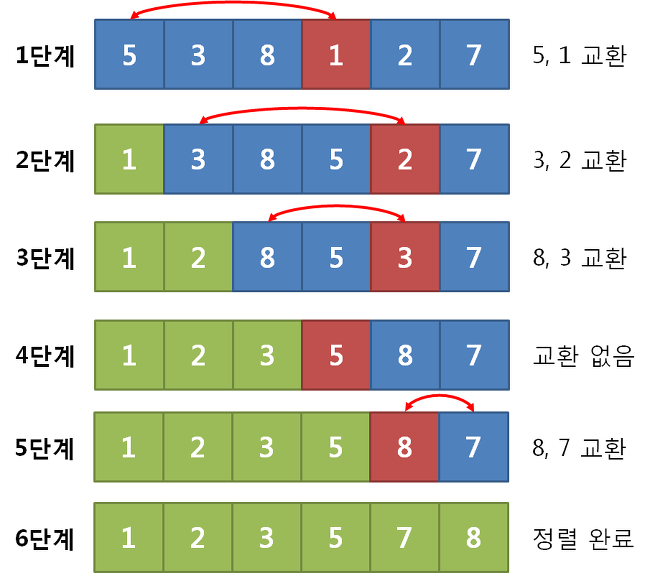
위의 과정을 하는 자세한 방법이다.
1단계. 우선 5, 4, 8, 1, 2, 7이 들어있는 배열을 준비합니다. 이 숫자중 가장 작은 숫자는 1이기에 1을 맨 앞의 숫자인 5와 교체하여 준다.
2단계. 1단계에서 확정된 1을 제외한 나머지 3, 8, 5, 2, 7중 가장 작은 수는 2이기 때문에 2와 가장 앞에 있는 숫자인 3을 교체하여 준다.
3단계. 마찬가지로 2단계에서 확정지은 2까지 숫자를 제외한 채 8, 5, 3, 7중 가장 작은 수는 3이기 때문에 3과 가장 앞에 있는 숫자인 8을 교체하여 준다.
=> 이렇게 정렬을 하게 되면 결국 6단계에서 1, 2, 3, 5, 7, 8 이 배열에 들어있게 되고 정렬이 끝나게 되는 것을 확인할 수 있다.
선택 정렬 구현 및 시간, 공간복잡도
void selectionSort(int[] arr) {
int indexMin, temp;
for (int i = 0; i < arr.length-1; i++) { // 1.
indexMin = i;
for (int j = i + 1; j < arr.length; j++) { // 2.
if (arr[j] < arr[indexMin]) { // 3.
indexMin = j;
}
} // 4.swap(arr[indexMin], arr[i])
temp = arr[indexMin];
arr[indexMin] = arr[i];
arr[i] = temp;
}
System.out.println(Arrays.toString(arr));
}
이 위의 코드처럼 선택정렬은 데이터가 n 개일 때,
첫번째 회전에서의 비교 횟수 : 1 ~ n-1 => n-1개
두번째 회전에서의 비교 횟수 : 2 ~ n-1 => n-2개
결국 n(n-1)/2개의 시간이 걸리게 되고 n개의 원소를 가진 배열을 정렬하는데 O(n^2) 만큼의 시간이 걸린다.
tip
최선, 평균, 최악의 경우 시간복잡도는 O(n^2)로 동일하다.
선택정렬은 주어진 배열 안에서 교환을 통하여 정렬이 되므로, 공간복잡도는 O(n) 이다.
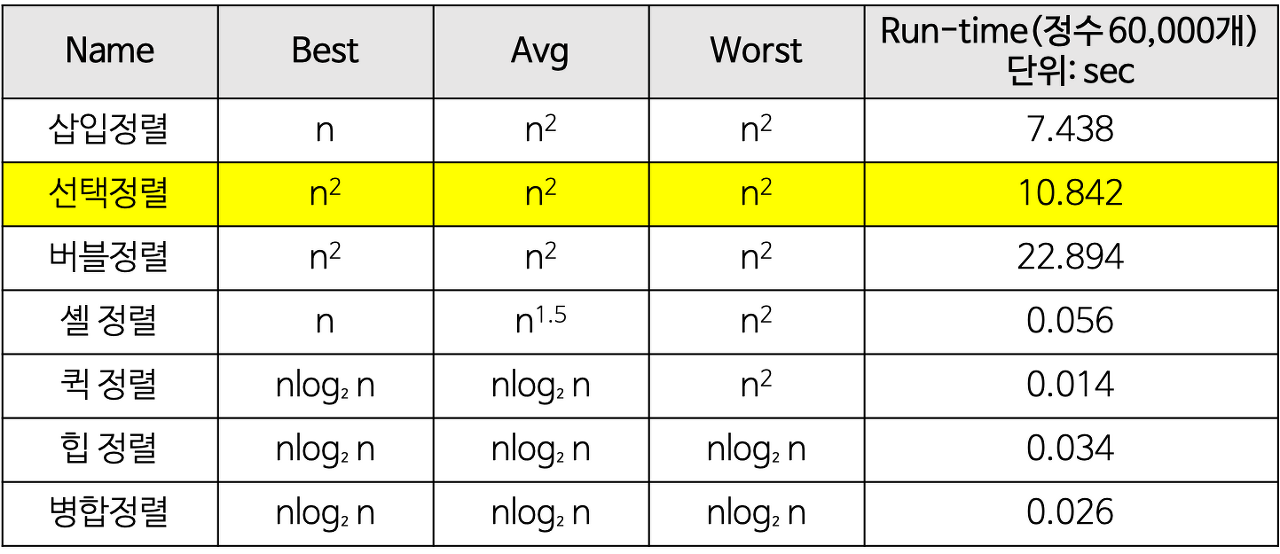
선택 정렬의 장단점
장점
- 알고리즘이 단순하다.
- 정렬을 위한 비교 횟수는 많지만, 거품 정렬에 비해서 교환하는 횟수가 적기 때문에 많은 교환이 일어나야 하는 자료에서는 효율적이다.
- 다른 메모리 공간이 필요하지 않는다.
단점
- 시간복잡도가 O(n^2)이므로 비효율적이다.
나올 수 있는 면접 질문
- 선택 정렬이란 무엇일까?
- 선택 정렬의 장단점은?
참고 url
기여자
HelloNaks
📦